机器学习：集成学习_梯度提升树
机器学习，集成学习，梯度提升树（Gradient Boosting Decision Tree）。在残差提升树的基础上，求残差近似值，结合线性回归损失函数梯度下降的方法，用负梯度表示残差近似值。残差与梯度是有区别的，残差可以有负值，但梯度不为负数，因为损失函数推导时都会求平方。
推导过程：
1、第一个基学习器：
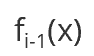
2、求损失函数：
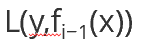
3、求得下一个基学习器：
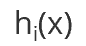
4、再求损失函数：
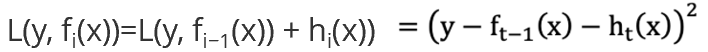
这个损失函数加上两个基学习器，相当于真实值减去了2个基学习器。另外结合损失函数最小二乘法的公式，最终求平方，这里就使得梯度的结果肯定不会是负数。另外，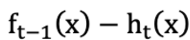
可以改写成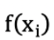
。
5、对损失函数求导（找导数为0的点，这个点最为接近残差）：
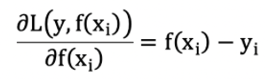
这里损失函数通过最小二乘法求得的是梯度，但是，残差 = 真实值 - 预测值，即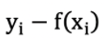
，刚好与梯度相反，那么要将公式转为残差可对公式加负号，得到负梯度：
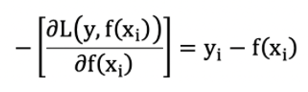
最后，梯度本身是处理线性回归问题，那么要处理分类问题时要转换为逻辑回归当中的log损失函数。