机器学习:梯度下降
梯度下降,形象表达类似于下山一点点往山底走,整个过程是一点点往下走,并且不可能完全到达最低点,只能接近最低点。在数学运算上,梯度下降用导数方式找出最小值,进而算出权重,最后得到模型的预测函数。
梯度下降也分单变量、多变量的情况。单变量找到最小值等于0的点求导,多变量则是求偏导。
梯度下降公式:
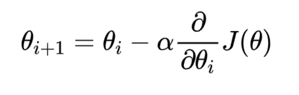
公式中的α称为学习率(机器学习:0.001~0.01),控制每次梯度下降的跨度(也可以说是快慢),跨度越大下降越快也越可能错过最小值,从而产生震荡,进一步发展成梯度爆炸现象。
梯度下降,使用导数的方式计算,相比于正规方程法采用矩阵运算,更适合处理大数据集,因此机器学习线性回归问题更多采用梯度下降。
尽管梯度下降采用求导的方法进行计算,但每次下降都计算全部样本得到下降梯度,计算量也是非常大的,所以梯度下降进一步产生了优化方案,即将这些算法方案分类,再按情况选择对应的算法进行计算。
全梯度下降算法 FGD
每次下降所有样本都参与计算。(梯度下降原始算法,计算量大)
随机梯度下降算法 SGD
每次下降随机选择一个样本参与计算。(一次参与样本过少,容易受异常值影响)
小批量梯度下降算法 mini-bantch
每次下降随机选择一批样本参与计算。(采用较高的算法,优化了大计算量、样本过少的问题)
随机平均梯度下降算法 SAG
每次下降取梯度平均值。(随机选一个样本算出梯度再与之前的梯度算平均值。该算法初期表现不一定好,因为刚开始参与的样本少,容易受异常值影响,所以平均值要经过一定次数的计算后才会表现稳定。)