机器学习_欠拟合与过拟合产生的原因
欠拟合、过拟合产生的原因,主要是与特征数量、样本的数据质量有关。
欠拟合
样本特征过少,不能有效的找到数据集的规律,模型预测产生欠拟合结果。
解决方法:增加样本特征项,通过特征工程去完善模型训练所需要的特征。
过拟合
样本特征过多,模型在训练集中表现过好,模型实际预测时反而不准确。
解决方法:基本方法可参照特征工程,选取关键特征或者合并一些特征。
总结:不管欠拟合还是过拟合问题,都要解决样本数据质量的问题,首先要对样本进行数据清洗保证数据符合要求,同时要使训练集中样本数量足够多,样本数过少,模型训练也难以收到好的效果,只有高质量并足够多的样本数据才能训练出达到拟合效果的模型。
正则化
对于过拟合问题,虽说是由于特征过多造成的,但真要由开发人员单方面进行特征工程有时是不现实的(因为开发人员只是模型建立工作中的一个环节),开发人员可通过正则化去解决过拟合问题(简单说就是通过数学计算方法处理特征,优化训练结果)。
正则化,在数学概念中属于向量运算的范数,范数分为L1、L2、Lp这几种计算方法(范数我理解是计算xy坐轴系上2点之间的距离,也就是在算向量的大小)。
为什么需要用正则化处理呢?首先回到损失函数,损失函数获取预测值与真实值之间的误差,算出权重w,最终得到预测函数。计算公式可写成:
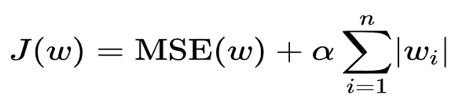
J(w)是损失函数,这里我理解为真实值与预测值之间的误差,属于已知数。
MSE(w)是均方误差,损失函数其中一种计算方式,我理解为已知训练集的xy(即特征、目标值)、但权重w未知的一元方程。
有了已知训练集xy未知权重w的一元方程,在其公式中加一个数(即正则化项),通过控制这个数的大小,从而影响权重w的大小,使权重接近于0或等于0,从而消除部分特征x对预测结果的影响。这就是正则化的计算方法。
MSE(w)公式如下:
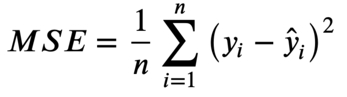
为什么正则化项可以消除部分特征呢?我是这样想的(多元线性回归,即多个特征值):
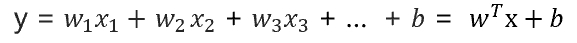
xy来源于训练集已知的,b推导可以合并到w中,最后只有w未知,那么只要使w靠近0或等于0就可以影响x的大小。
进一步说,误差等于MSE加上正则化项,误差已知、训练集xy已知、正则化项人为控制已知,MSE中只有权重w未知,那么正则化项的大小就直接影响权重w的大小,权重w接近0或等于0可改变特征x在预测中的作用大小,即达到过拟合时减少特征项的目的。
正则化项,有两种:L1、L2。以L1为例:
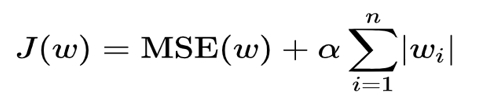
α称为惩罚系数,是人为指定的超参数,后面部分可以理解为w权重加总。当惩罚系数越大,MSE中的w则越接近0、越可能消除特征项。
L2正则化:
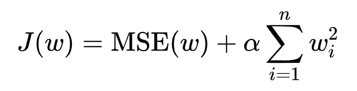
L1与L2的不同点在于,L1可以使w等于0,但L2只能接近0。