机器学习:逻辑回归_数学基础
机器学习,逻辑回归,数学基础。机器学习分为:有监督学习、无监督学习、部分有监督学习、强化学习。有监督学习要处理两类问题:分类问题、回归问题。逻辑回归用于处理分类问题中的二分类问题。二分类问题只有两种答案,比如:有病或无病(只有两种结果,不会有亚健康这种说法)。
结合数学函数进行计算,逻辑回归结果在(0,1)的范围,进而得出更接近0或是1的预测结果,因此逻辑回归不同于线性回归评估模型准确率,逻辑回归是概率问题。
sigmoid函数
作为逻辑回归的计算函数(激活函数,我觉得说在计算容易明白),sigmoid函数有几个特性要知道。
公式:
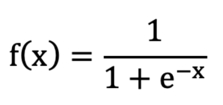
函数图:
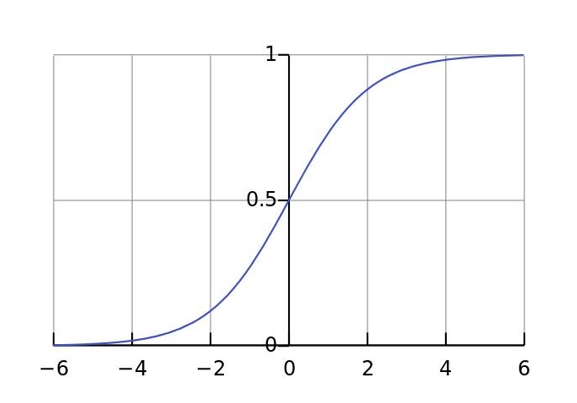
x坐标轴(-∞, +∞),sigmoid函数计算后会将结果映射在(0,1)范围内。
拐点(x=0,y=0.5)。
联合概率
联合概率是将两个或多个相同事件发生的概率相乘,积就是联合概率,表示两个或多个事件同时发生的概率。什么事件适合计算联合概率?相同事件可以计算联合概率,比如星期一早餐喝豆浆的概率,星期二早餐喝豆浆的概率,计算星期一、星期二都喝豆浆的概率。
条件概率
条件概率是将两个或多个不相同事件发生的概率相乘,积就是条件概率,表示一个事件发生后再发生另一个事件的概率。比如星期一早餐喝豆浆的概率,中午吃面的概率,计算喝豆浆又吃面的概率。
极大似然估计
极大似然估计,通过观测结果去估计未知比率(称为参数,不过我觉得比率容易理解)。简单例子:袋子里有一些球,抽出来5个球,1个红色4个绿色,那么袋子里绿球占比4/5。机器学习中,观测结果就是训练集。
极大似然估计,在数学计算时,先将要求的参数设为未知数,结合联合概率或条件概率去组成计算公式,对公式求导得到计算结果,再估计未知参数(也就是这个事件发生的概率,要注意逻辑回归的激活函数映射范围在(0,1)之间,因此未知参数也属于该范围内)。
对数函数
a的b次方等于N,b就是以a为底N的对数。
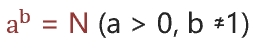
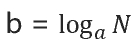
对数性质:
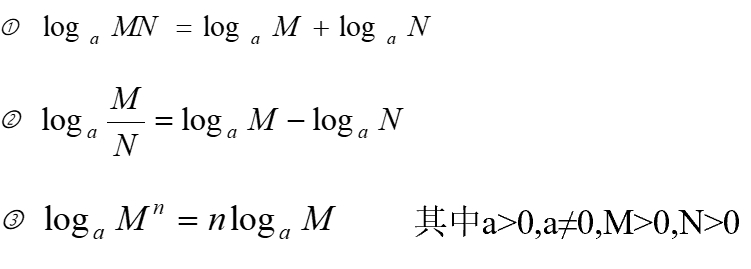
对数函数可应用于概率计算,如将联合概率相乘改为对数相加。